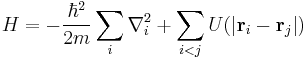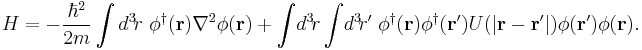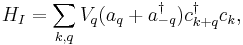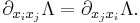Quantum field theory
| Quantum field theory | ||||||||||||||
 |
||||||||||||||
| (Feynman diagram) | ||||||||||||||
History of...
|
||||||||||||||
Quantum field theory (QFT)[1] provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized (represented) by an infinite number of dynamical degrees of freedom, that is, fields and (in a condensed matter context) many-body systems. It is the natural and quantitative language of particle physics and condensed matter physics. Most theories in modern particle physics, including the Standard Model of elementary particles and their interactions, are formulated as relativistic quantum field theories. Quantum field theories are used in many contexts, elementary particle physics being the most vital example, where the particle count/number going into a reaction fluctuates and changes, differing from the count/number going out, for example, and for the description of critical phenomena and quantum phase transitions, such as in the BCS theory of superconductivity, also see phase transition, quantum phase transition, critical phenomena. Quantum field theory is thought by many to be the unique and correct outcome of combining the rules of quantum mechanics with special relativity.
In perturbative quantum field theory, the forces between particles are mediated by other particles. The electromagnetic force between two electrons is caused by an exchange of photons. Intermediate vector bosons mediate the weak force and gluons mediate the strong force. There is currently no complete quantum theory of the remaining fundamental force, gravity, but many of the proposed theories postulate the existence of a graviton particle that mediates it. These force-carrying particles are virtual particles and, by definition, cannot be detected while carrying the force, because such detection will imply that the force is not being carried. In addition, the notion of "force mediating particle" comes from perturbation theory, and thus does not make sense in a context of bound states.
In QFT photons are not thought of as 'little billiard balls', they are considered to be field quanta - necessarily chunked ripples in a field, or "excitations," that 'look like' particles. Fermions, like the electron, can also be described as ripples/excitations in a field, where each kind of fermion has its own field. In summary, the classical visualisation of "everything is particles and fields," in quantum field theory, resolves into "everything is particles," which then resolves into "everything is fields." In the end, particles are regarded as excited states of a field (field quanta). The gravitational field and the electromagnetic field are the only two fundamental fields in Nature that have infinite range and a corresponding classical low-energy limit, which greatly diminishes and hides their "particle-like" excitations. Albert Einstein, in 1905, attributed "particle-like" and discrete exchanges of momenta and energy, characteristic of "field quanta," to the electromagnetic field. Originally, his principal motivation was to explain the thermodynamics of radiation. Although it is often claimed that the photoelectric and Compton effects require a quantum description of the EM field, this is now understood to be untrue, and proper proof of the quantum nature of radiation is now taken up into modern quantum optics as in the antibunching effect[2]. The word "photon" was coined in 1926 by the great physical chemist Gilbert Newton Lewis (see also the articles photon antibunching and laser).
The "low-energy limit" of the correct quantum field-theoretic description of the electromagnetic field, quantum electrodynamics, is believed to become James Clerk Maxwell's 1864 theory, although the "classical limit" of quantum electrodynamics has not been as widely explored as that of quantum mechanics. Presumably, the as yet unknown correct quantum field-theoretic treatment of the gravitational field will become and "look exactly like" Einstein's general theory of relativity in the "low-energy limit." Indeed, quantum field theory itself is quite possibly the low-energy-effective-field-theory limit of a more fundamental theory such as superstring theory. Compare in this context the article effective field theory.
Contents
|
History
Quantum field theory originated in the 1920s from the problem of creating a quantum mechanical theory of the electromagnetic field. In 1926 Max Born, Pascual Jordan, and Werner Heisenberg constructed such a theory by expressing the field's internal degrees of freedom as an infinite set of harmonic oscillators and by employing the usual procedure for quantizing those oscillators (canonical quantization). Max Planck, a physicist at the University of Kiels, observed the behavior at the atomic level of radiation and heat on matter. He observed that the energy absorbed or emitted was contained in small, discrete (i.e. individual) energy packets called quanta. This theory assumed that no electric charges or currents were present, and today would be called a free field theory. The first reasonably complete theory of quantum electrodynamics, which included both the electromagnetic field and electrically charged matter (specifically, electrons) as quantum mechanical objects, was created by Paul Dirac in 1927.[3] This quantum field theory could be used to model important processes such as the emission of a photon by an electron dropping into a quantum state of lower energy, a process in which the number of particles changes — one atom in the initial state becomes an atom plus a photon in the final state. It is now understood that the ability to describe such processes is one of the most important features of quantum field theory.
It was evident from the beginning that a proper quantum treatment of the electromagnetic field had to somehow incorporate Einstein's relativity theory, which had after all grown out of the study of classical electromagnetism. This need to put together relativity and quantum mechanics was the second major motivation in the development of quantum field theory. Pascual Jordan and Wolfgang Pauli showed in 1928 that quantum fields could be made to behave in the way predicted by special relativity during coordinate transformations (specifically, they showed that the field commutators were Lorentz invariant). A further boost for quantum field theory came with the discovery of the Dirac equation, which was originally formulated and interpreted as a single-particle equation analogous to the Schrödinger equation, but unlike the Schrödinger equation, the Dirac equation satisfies both Lorentz invariance, that is, the requirements of special relativity, and the rules of quantum mechanics. The Dirac equation accommodated the spin-1/2 value of the electron and accounted for its magnetic moment as well as giving accurate predictions for the spectra of hydrogen. The attempted interpretation of the Dirac equation as a single-particle equation could not be maintained long, however, and finally it was shown that several of its undesirable properties (such as negative-energy states) could be made sense of by reformulating and reinterpreting the Dirac equation as a true field equation, in this case for the quantized "Dirac field" or the "electron field", with the "negative-energy solutions" pointing to the existence of anti-particles. This work was performed first by Dirac himself with the invention of hole theory 1930 and also by Wendell Furry, Robert Oppenheimer, Vladimir Fock, and others. Schrödinger, during the same period that he discovered his famous equation in 1926, also independently found the relativistic generalization of it known as the Klein-Gordon equation but dismissed it since, without spin, it predicted impossible properties for the hydrogen spectrum. See Oskar Klein, Walter Gordon. All relativistic wave equations that describe spin-zero particles are said to be of the Klein-Gordon type.
A subtle and careful analysis in 1933 and later in 1950 by Niels Bohr and Leon Rosenfeld showed that there is a fundamental limitation on the ability to simultaneously measure the electric and magnetic field strengths that enter into the description of charges in interaction with radiation, imposed by the uncertainty principle, which must apply to all canonically conjugate quantities. This limitation is crucial for the successful formulation and interpretation of a quantum field theory of photons and electrons(quantum electrodynamics),and indeed,any perturbative quantum field theory. The analysis of Bohr and Rosenfeld explains fluctuations in the values of the electromagnetic field that differ from the classically "allowed" values distant from the sources of the field. Their analysis was crucial to showing that the limitations and physical implications of the uncertainty principle apply to all dynamical systems, whether fields or material particles. Their analysis also convinced most people that any notion of returning to a fundamental description of nature based on classical field theory, such as what Einstein aimed at with his numerous and failed attempts at a classical unified field theory, was simply out of the question.
The third thread in the development of quantum field theory was the need to handle the statistics of many-particle systems consistently and with ease. In 1927 Jordan tried to extend the canonical quantization of fields to the many-body wave functions of identical particles, a procedure that is sometimes called second quantization. In 1928, Jordan and Eugene Wigner found that the quantum field describing electrons, or other fermions, had to be expanded using anti-commuting creation and annihilation operators due to the Pauli exclusion principle. This thread of development was incorporated into many-body theory and strongly influenced condensed matter physics and nuclear physics.
Despite its early successes quantum field theory was plagued by several serious theoretical difficulties. Basic physical quantities, such as the self-energy of the electron, the energy shift of electron states due to the presence of the electromagnetic field, gave infinite, divergent contributions — a nonsensical result — when computed using the perturbative techniques available in the 1930s and most of the 1940s. The electron self-energy problem was already a serious issue in the classical electromagnetic field theory, where the attempt to attribute to the electron a finite size or extent (the classical electron-radius) led immediately to the question of what non-electromagnetic stresses would need to be invoked, which would presumably hold the electron together against the Coulomb repulsion of its finite-sized "parts". The situation was dire, and had certain features that reminded many of the "Rayleigh-Jeans difficulty", which drove Max Planck along the inevitable path to his law of black-body radiation. What made the situation in the 1940s so desperate and gloomy, however, was the fact that the correct ingredients (the second-quantized Maxwell-Dirac field equations) for the theoretical description of interacting photons and electrons were well in place, and no major conceptual change was needed analogous to that which was necessitated by a finite and physically sensible account of the radiative behavior of hot objects, as provided by the Planck radiation law.
A notable exception during the 1940s was made by John Wheeler and Richard Feynman, who attempted a reformulation of electrodynamics with their so-called Wheeler-Feynman absorber theory of radiation. This questioned the field theory approach to "local action", that is, the approach that involves causes preceding their effects in the way demanded by the special theory of relativity, the upper-limit of the speed of transmission of an interaction being the light-velocity. The absorber theory attempted to eliminate the traditional local-contiguous field concept completely from the description of the matter/radiation interaction using a model involving half "incoming" and half "outgoing" (half retarded/half advanced) time-symmetric components of a "radiation field" that was, in effect, an action-at-a-distance construct. The main motivation behind this program was the desire to eliminate the self-energy infinity and the "radiation-reaction" infinity for the electron (positron). In this approach, a single charge does not produce a field of its own, hence, it has no self-energy, its "field" being due to its instantaneous action-at-a-distance with all other charges in the Universe. This type of interaction can be formulated in a Lorentz covariant manner.
No matter how enchanting the "absorber theory" was ultimately, however, it was getting from the lofty heights of field theory, which most theorists trusted to be foundationally correct (the ingredients we have in mind in the present case are:the second-quantized Maxwell-Dirac field equations. See:Canonical quantization), to being able to calculate practical, finite answers to simple questions, rather than getting catastrophically divergent answers even in the lowest-order, and which could then be compared to experiment, where the rubber-meets-the-road. Taming the infinities was what was so desperately needed, and this could only follow from correctly identifying their nature and developing the mathematical techniques necessary to taming them.
This "divergence problem" was solved in the case of quantum electrodynmaics during the late 1940s and early 1950s by Hans Bethe, Tomonaga, Schwinger, Feynman, and Dyson, through the procedure known as renormalization. Great progress was made after realizing that ALL infinities in quantum electrodynamics are related to two effects: the self-energy of the electron/positron and vacuum polarization. Renormalization concerns the business of paying very careful attention to just what is meant by, for example, the very concepts "charge" and "mass" as they occur in the pure, non-interacting field-equations. The "vacuum" is itself polarizable and, hence, populated by virtual particle (on shell and off shell) pairs, and, hence, is a seething and busy dynamical system in its own right. This was a critical step in identifying the source of "infinities" and "divergences". The "bare mass" and the "bare charge" of a particle, the values that appear in the free-field equations (non-interacting case), are abstractions that are simply not realized in experiment (in interaction). What we measure, and hence, what we must take account of with our equations, and what the solutions must account for, are the "renormalized mass" and the "renormalized charge" of a particle. That is to say, the "shifted" or "dressed" values these quantities must have when due care is taken to include all deviations from their "bare values" is dictated by the very nature of quantum fields themselves.
The first approach that bore fruit is known as the "interaction representation," (see the article Interaction picture) a Lorentz covariant and gauge-invariant generalization of time-dependent perturbation theory used in ordinary quantum mechanics, and developed by Tomonaga and Schwinger, generalizing earlier efforts of Dirac, Fock and Podolsky. Tomonaga and Schwinger invented a relativistically covariant scheme for representing field commutators and field operators intermediate between the two main representations of a quantum system, the Schrödinger and the Heisenberg representations (see the article on quantum mechanics). Within this scheme, field commutators at separated points can be evaluated in terms of "bare" field creation and annihilation operators. This allows for keeping track of the time-evolution of both the "bare" and "renormalized", or perturbed, values of the Hamiltonian and expresses everything in terms of the coupled, gauge invariant "bare" field-equations. Schwinger gave the most elegant formulation of this approach. The next and most famous development is due to Feynman, who, with his brilliant rules for assigning a "graph"/"diagram" to the terms in the scattering matrix (See S-Matrix Feynman diagrams). These directly corresponded (through the Schwinger-Dyson equation) to the measurable physical processes (cross sections, probability amplitudes, decay widths and lifetimes of excited states) one needs to be able to calculate. This revolutionized how quantum field theory calculations are carried-out in practice.
Two classic text-books from the 1960s, J.D. Bjorken and S.D. Drell, Relativistic Quantum Mechanics (1964) and J.J. Sakurai, Advanced Quantum Mechanics (1967), thoroughly developed the Feynman graph expansion techniques using physically intuitive and practical methods following from the correspondence principle, without worrying about the technicalities involved in deriving the Feynman rules from the superstructure of quantum field theory itself. Although both Feynman's heuristic and pictorial style of dealing with the infinities, as well as the formal methods of Tomonaga and Schwinger, worked extremely well, and gave spectacularly accurate answers, the true analytical nature of the question of "renormalizability", that is, whether ANY theory formulated as a "quantum field theory" would give finite answers, was not worked-out till much later, when the urgency of trying to formulate finite theories for the strong and electro-weak (and gravitational interactions) demanded its solution.
Renormalization in the case of QED was largely fortuitous due to the smallness of the coupling constant, the fact that the coupling has no dimensions involving mass, the so-called fine structure constant, and also the zero-mass of the gauge boson involved, the photon, rendered the small-distance/high-energy behavior of QED manageable. Also, electromagnetic processess are very "clean" in the sense that they are not badly suppressed/damped and/or hidden by the other gauge interactions. By 1958 Sidney Drell observed: "Quantum electrodynamics (QED) has achieved a status of peaceful coexistence with its divergences...."
The unification of the electromagnetic force with the weak force encountered initial difficulties due to the lack of accelerator energies high enough to reveal processes beyond the Fermi interaction range. Additionally, a satisfactory theoretical understanding of hadron substructure had to be developed, culminating in the quark model.
In the case of the strong interactions, progress concerning their short-distance/high-energy behavior was much slower and more frustrating. For strong interactions with the electro-weak fields, there were difficult issues regarding the strength of coupling, the mass generation of the force carriers as well as their non-linear, self interactions. Although there has been theoretical progress toward a grand unified quantum field theory incorporating the electro-magnetic force, the weak force and the strong force, empirical verification is still pending. Superunification, incorporating the gravitational force, is still very speculative, and is under intensive investigation by many of the best minds in contemporary theoretical physics. Gravitation is a tensor field description of a spin-2 gauge-boson, the "graviton", and is further discussed in the articles on general relativity and quantum gravity.
From the point of view of the techniques of (four-dimensional) quantum field theory, and as the numerous and heroic efforts to formulate a consistent quantum gravity theory by some very able minds attests, gravitational quantization was, and is still, the reigning champion for bad behavior. There are problems and frustrations stemming from the fact that the gravitational coupling constant has dimensions involving inverse powers of mass, and as a simple consequence, it is plagued by badly behaved (in the sense of perturbation theory) non-linear and violent self-interactions. Gravity, basically, gravitates, which in turn...gravitates...and so on, (i.e., gravity is itself a source of gravity,...,) thus creating a nightmare at all orders of perturbation theory. Also, gravity couples to all energy equally strongly, as per the equivalence principle, so this makes the notion of ever really "switching-off", "cutting-off" or separating, the gravitational interaction from other interactions ambiguous and impossible since, with gravitation, we are dealing with the very structure of space-time itself. (See general covariance and, for a modest, yet highly non-trivial and significant interplay between (QFT) and gravitation (spacetime), see the article Hawking radiation and references cited therein. Also quantum field theory in curved spacetime).
Thanks to the somewhat brute-force, clanky and heuristic methods of Feynman, and the elegant and abstract methods of Tomonaga/Schwinger, from the period of early renormalization, we do have the modern theory of quantum electrodynamics (QED). It is still the most accurate physical theory known, the prototype of a successful quantum field theory. Beginning in the 1950s with the work of Yang and Mills, as well as Ryoyu Utiyama, following the previous lead of Weyl and Pauli, deep explorations illuminated the types of symmetries and invariances any field theory must satisfy. QED, and indeed, all field theories, were generalized to a class of quantum field theories known as gauge theories. Quantum electrodynamics is the most famous example of what is known as an Abelian gauge theory. It relies on the symmetry group U(1) and has one massless gauge field, the U(1) gauge symmetry, dictating the form of the interactions involving the electromagnetic field, with the photon being the gauge boson. That symmetries dictate, limit and necessitate the form of interaction between particles is the essence of the "gauge theory revolution." Yang and Mills formulated the first explicit example of a non-Abelian gauge theory, Yang-Mills theory, with an attempted explanation of the strong interactions in mind. The strong interactions were then (incorrectly) understood in the mid-1950s, to be mediated by the pi-mesons, the particles predicted by Hideki Yukawa in 1935, based on his profound reflections concerning the reciprocal connection between the mass of any force-mediating particle and the range of the force it mediates. This was allowed by the uncertainty principle. The 1960s and 1970s saw the formulation of a gauge theory now known as the Standard Model of particle physics, which systematically describes the elementary particles and the interactions between them.
The electroweak interaction part of the standard model was formulated by Sheldon Glashow in the years 1958-60 with his discovery of the SU(2)xU(1) group structure of the theory. Steven Weinberg and Abdus Salam brilliantly invoked the Higgs–Brout–Englert–Guralnik–Hagen–Kibble mechanism for the generation of the W's and Z masses (the intermediate vector boson(s) responsible for the weak interactions and neutral-currents) and keeping the mass of the photon zero. The Goldstone/Higgs idea for generating mass in gauge theories was sparked in the late 1950s and early 1960s when a number of theoreticians (including Yoichiro Nambu, Steven Weinberg, Jeffrey Goldstone, François Englert, Robert Brout, G. S. Guralnik, C. R. Hagen, Tom Kibble and Philip Warren Anderson) noticed a possibly useful analogy to the (spontaneous) breaking of the U(1) symmetry of electromagnetism in the formation of the BCS ground-state of a superconductor. The gauge boson involved in this situation, the photon, behaves as though it has acquired a finite mass. There is a further possibility that the physical vacuum (ground-state) does not respect the symmetries implied by the "unbroken" electroweak Lagrangian (see the article Electroweak interaction for more details) from which one arrives at the field equations. The electroweak theory of Weinberg and Salam was shown to be renormalizable (finite) and hence consistent by Gerardus 't Hooft and Martinus Veltman. The Glashow-Weinberg-Salam theory (GWS-Theory) is a triumph and, in certain applications, gives an accuracy on a par with quantum electrodynamics.
Also during the 1970s parallel developments in the study of phase transitions in condensed matter physics led Leo Kadanoff, Michael Fisher and Kenneth Wilson (extending work of Ernst Stueckelberg, Andre Peterman, Murray Gell-Mann, and Francis Low) to a set of ideas and methods known as the renormalization group. By providing a better physical understanding of the renormalization procedure invented in the 1940s, the renormalization group sparked what has been called the "grand synthesis" of theoretical physics, uniting the quantum field theoretical techniques used in particle physics and condensed matter physics into a single theoretical framework.
The study of quantum field theory is alive and flourishing, as are applications of this method to many physical problems. It remains one of the most vital areas of theoretical physics today, providing a common language to many branches of physics.
Principles of quantum field theory
Classical fields and quantum fields
Quantum mechanics, in its most general formulation, is a theory of abstract operators (observables) acting on an abstract state space (Hilbert space), where the observables represent physically observable quantities and the state space represents the possible states of the system under study. Furthermore, each observable corresponds, in a technical sense, to the classical idea of a degree of freedom. For instance, the fundamental observables associated with the motion of a single quantum mechanical particle are the position and momentum operators  and
and  . Ordinary quantum mechanics deals with systems such as this, which possess a small set of degrees of freedom.
. Ordinary quantum mechanics deals with systems such as this, which possess a small set of degrees of freedom.
(It is important to note, at this point, that this article does not use the word "particle" in the context of wave–particle duality. In quantum field theory, "particle" is a generic term for any discrete quantum mechanical entity, such as an electron or photon, which can behave like classical particles or classical waves under different experimental conditions.)
A quantum field is a quantum mechanical system containing a large, and possibly infinite, number of degrees of freedom. A classical field contains a set of degrees of freedom at each point of space; for instance, the classical electromagnetic field defines two vectors — the electric field and the magnetic field — that can in principle take on distinct values for each position  . When the field as a whole is considered as a quantum mechanical system, its observables form an infinite (in fact uncountable) set, because
. When the field as a whole is considered as a quantum mechanical system, its observables form an infinite (in fact uncountable) set, because  is continuous.
is continuous.
Furthermore, the degrees of freedom in a quantum field are arranged in "repeated" sets. For example, the degrees of freedom in an electromagnetic field can be grouped according to the position  , with exactly two vectors for each
, with exactly two vectors for each  . Note that
. Note that  is an ordinary number that "indexes" the observables; it is not to be confused with the position operator
is an ordinary number that "indexes" the observables; it is not to be confused with the position operator  encountered in ordinary quantum mechanics, which is an observable. (Thus, ordinary quantum mechanics is sometimes referred to as "zero-dimensional quantum field theory", because it contains only a single set of observables.)
encountered in ordinary quantum mechanics, which is an observable. (Thus, ordinary quantum mechanics is sometimes referred to as "zero-dimensional quantum field theory", because it contains only a single set of observables.)
It is also important to note that there is nothing special about  because, as it turns out, there is generally more than one way of indexing the degrees of freedom in the field.
because, as it turns out, there is generally more than one way of indexing the degrees of freedom in the field.
In the following sections, we will show how these ideas can be used to construct a quantum mechanical theory with the desired properties. We will begin by discussing single-particle quantum mechanics and the associated theory of many-particle quantum mechanics. Then, by finding a way to index the degrees of freedom in the many-particle problem, we will construct a quantum field and study its implications.
Single-particle and many-particle quantum mechanics
In quantum mechanics, the time-dependent Schrödinger equation for a single particle is
where  is the particle's mass,
is the particle's mass, 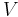 is the applied potential, and
is the applied potential, and 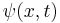 denotes the wavefunction.
denotes the wavefunction.
We wish to consider how this problem generalizes to  particles. There are two motivations for studying the many-particle problem. The first is a straightforward need in condensed matter physics, where typically the number of particles is on the order of Avogadro's number (6.0221415 x 1023). The second motivation for the many-particle problem arises from particle physics and the desire to incorporate the effects of special relativity. If one attempts to include the relativistic rest energy into the above equation (in quantum mechanics where position is an observable), the result is either the Klein-Gordon equation or the Dirac equation. However, these equations have many unsatisfactory qualities; for instance, they possess energy eigenvalues that extend to –∞, so that there seems to be no easy definition of a ground state. It turns out that such inconsistencies arise from relativistic wavefunctions having a probabilistic interpretation in position space, as probability conservation is not a relativistically covariant concept. In quantum field theory, unlike in quantum mechanics, position is not an observable, and thus, one does not need the concept of a position-space probability density. For quantum fields whose interaction can be treated perturbatively, this is equivalent to neglecting the possibility of dynamically creating or destroying particles, which is a crucial aspect of relativistic quantum theory. Einstein's famous mass-energy relation allows for the possibility that sufficiently massive particles can decay into several lighter particles, and sufficiently energetic particles can combine to form massive particles. For example, an electron and a positron can annihilate each other to create photons. This suggests that a consistent relativistic quantum theory should be able to describe many-particle dynamics.
particles. There are two motivations for studying the many-particle problem. The first is a straightforward need in condensed matter physics, where typically the number of particles is on the order of Avogadro's number (6.0221415 x 1023). The second motivation for the many-particle problem arises from particle physics and the desire to incorporate the effects of special relativity. If one attempts to include the relativistic rest energy into the above equation (in quantum mechanics where position is an observable), the result is either the Klein-Gordon equation or the Dirac equation. However, these equations have many unsatisfactory qualities; for instance, they possess energy eigenvalues that extend to –∞, so that there seems to be no easy definition of a ground state. It turns out that such inconsistencies arise from relativistic wavefunctions having a probabilistic interpretation in position space, as probability conservation is not a relativistically covariant concept. In quantum field theory, unlike in quantum mechanics, position is not an observable, and thus, one does not need the concept of a position-space probability density. For quantum fields whose interaction can be treated perturbatively, this is equivalent to neglecting the possibility of dynamically creating or destroying particles, which is a crucial aspect of relativistic quantum theory. Einstein's famous mass-energy relation allows for the possibility that sufficiently massive particles can decay into several lighter particles, and sufficiently energetic particles can combine to form massive particles. For example, an electron and a positron can annihilate each other to create photons. This suggests that a consistent relativistic quantum theory should be able to describe many-particle dynamics.
Furthermore, we will assume that the  particles are indistinguishable. As described in the article on identical particles, this implies that the state of the entire system must be either symmetric (bosons) or antisymmetric (fermions) when the coordinates of its constituent particles are exchanged. These multi-particle states are rather complicated to write. For example, the general quantum state of a system of
particles are indistinguishable. As described in the article on identical particles, this implies that the state of the entire system must be either symmetric (bosons) or antisymmetric (fermions) when the coordinates of its constituent particles are exchanged. These multi-particle states are rather complicated to write. For example, the general quantum state of a system of  bosons is written as
bosons is written as
where 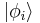 are the single-particle states,
are the single-particle states, 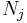 is the number of particles occupying state
is the number of particles occupying state  , and the sum is taken over all possible permutations
, and the sum is taken over all possible permutations  acting on
acting on  elements. In general, this is a sum of
elements. In general, this is a sum of 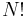 (
( factorial) distinct terms, which quickly becomes unmanageable as
factorial) distinct terms, which quickly becomes unmanageable as  increases. The way to simplify this problem is to turn it into a quantum field theory.
increases. The way to simplify this problem is to turn it into a quantum field theory.
Second quantization
In this section, we will describe a method for constructing a quantum field theory called second quantization. This basically involves choosing a way to index the quantum mechanical degrees of freedom in the space of multiple identical-particle states. It is based on the Hamiltonian formulation of quantum mechanics; several other approaches exist, such as the Feynman path integral,[4] which uses a Lagrangian formulation. For an overview, see the article on quantization.
Second quantization of bosons
For simplicity, we will first discuss second quantization for bosons, which form perfectly symmetric quantum states. Let us denote the mutually orthogonal single-particle states by 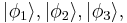 and so on. For example, the 3-particle state with one particle in state
and so on. For example, the 3-particle state with one particle in state 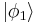 and two in state
and two in state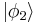 is
is
The first step in second quantization is to express such quantum states in terms of occupation numbers, by listing the number of particles occupying each of the single-particle states 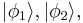 etc. This is simply another way of labelling the states. For instance, the above 3-particle state is denoted as
etc. This is simply another way of labelling the states. For instance, the above 3-particle state is denoted as
The next step is to expand the  -particle state space to include the state spaces for all possible values of
-particle state space to include the state spaces for all possible values of  . This extended state space, known as a Fock space, is composed of the state space of a system with no particles (the so-called vacuum state), plus the state space of a 1-particle system, plus the state space of a 2-particle system, and so forth. It is easy to see that there is a one-to-one correspondence between the occupation number representation and valid boson states in the Fock space.
. This extended state space, known as a Fock space, is composed of the state space of a system with no particles (the so-called vacuum state), plus the state space of a 1-particle system, plus the state space of a 2-particle system, and so forth. It is easy to see that there is a one-to-one correspondence between the occupation number representation and valid boson states in the Fock space.
At this point, the quantum mechanical system has become a quantum field in the sense we described above. The field's elementary degrees of freedom are the occupation numbers, and each occupation number is indexed by a number 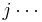 , indicating which of the single-particle states
, indicating which of the single-particle states 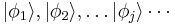 it refers to.
it refers to.
The properties of this quantum field can be explored by defining creation and annihilation operators, which add and subtract particles. They are analogous to "ladder operators" in the quantum harmonic oscillator problem, which added and subtracted energy quanta. However, these operators literally create and annihilate particles of a given quantum state. The bosonic annihilation operator  and creation operator
and creation operator 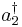 have the following effects:
have the following effects:
It can be shown that these are operators in the usual quantum mechanical sense, i.e. linear operators acting on the Fock space. Furthermore, they are indeed Hermitian conjugates, which justifies the way we have written them. They can be shown to obey the commutation relation
where  stands for the Kronecker delta. These are precisely the relations obeyed by the ladder operators for an infinite set of independent quantum harmonic oscillators, one for each single-particle state. Adding or removing bosons from each state is therefore analogous to exciting or de-exciting a quantum of energy in a harmonic oscillator.
stands for the Kronecker delta. These are precisely the relations obeyed by the ladder operators for an infinite set of independent quantum harmonic oscillators, one for each single-particle state. Adding or removing bosons from each state is therefore analogous to exciting or de-exciting a quantum of energy in a harmonic oscillator.
The Hamiltonian of the quantum field (which, through the Schrödinger equation, determines its dynamics) can be written in terms of creation and annihilation operators. For instance, the Hamiltonian of a field of free (non-interacting) bosons is
where 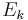 is the energy of the
is the energy of the 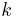 -th single-particle energy eigenstate. Note that
-th single-particle energy eigenstate. Note that
Second quantization of fermions
It turns out that a different definition of creation and annihilation must be used for describing fermions. According to the Pauli exclusion principle, fermions cannot share quantum states, so their occupation numbers 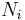 can only take on the value 0 or 1. The fermionic annihilation operators
can only take on the value 0 or 1. The fermionic annihilation operators  and creation operators
and creation operators 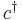 are defined by their actions on a Fock state thus
are defined by their actions on a Fock state thus
These obey an anticommutation relation:
One may notice from this that applying a fermionic creation operator twice gives zero, so it is impossible for the particles to share single-particle states, in accordance with the exclusion principle.
Field operators
We have previously mentioned that there can be more than one way of indexing the degrees of freedom in a quantum field. Second quantization indexes the field by enumerating the single-particle quantum states. However, as we have discussed, it is more natural to think about a "field", such as the electromagnetic field, as a set of degrees of freedom indexed by position.
To this end, we can define field operators that create or destroy a particle at a particular point in space. In particle physics, these operators turn out to be more convenient to work with, because they make it easier to formulate theories that satisfy the demands of relativity.
Single-particle states are usually enumerated in terms of their momenta (as in the particle in a box problem.) We can construct field operators by applying the Fourier transform to the creation and annihilation operators for these states. For example, the bosonic field annihilation operator 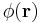 is
is
The bosonic field operators obey the commutation relation
where 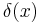 stands for the Dirac delta function. As before, the fermionic relations are the same, with the commutators replaced by anticommutators.
stands for the Dirac delta function. As before, the fermionic relations are the same, with the commutators replaced by anticommutators.
It should be emphasized that the field operator is not the same thing as a single-particle wavefunction. The former is an operator acting on the Fock space, and the latter is a quantum-mechanical amplitude for finding a particle in some position. However, they are closely related, and are indeed commonly denoted with the same symbol. If we have a Hamiltonian with a space representation, say
where the indices  and
and  run over all particles, then the field theory Hamiltonian is
run over all particles, then the field theory Hamiltonian is
This looks remarkably like an expression for the expectation value of the energy, with  playing the role of the wavefunction. This relationship between the field operators and wavefunctions makes it very easy to formulate field theories starting from space-projected Hamiltonians.
playing the role of the wavefunction. This relationship between the field operators and wavefunctions makes it very easy to formulate field theories starting from space-projected Hamiltonians.
Implications of quantum field theory
Unification of fields and particles
The "second quantization" procedure that we have outlined in the previous section takes a set of single-particle quantum states as a starting point. Sometimes, it is impossible to define such single-particle states, and one must proceed directly to quantum field theory. For example, a quantum theory of the electromagnetic field must be a quantum field theory, because it is impossible (for various reasons) to define a wavefunction for a single photon. In such situations, the quantum field theory can be constructed by examining the mechanical properties of the classical field and guessing the corresponding quantum theory. For free (non-interacting) quantum fields, the quantum field theories obtained in this way have the same properties as those obtained using second quantization, such as well-defined creation and annihilation operators obeying commutation or anticommutation relations.
Quantum field theory thus provides a unified framework for describing "field-like" objects (such as the electromagnetic field, whose excitations are photons) and "particle-like" objects (such as electrons, which are treated as excitations of an underlying electron field), so long as one can treat interactions as "perturbations" of free fields. There are still unsolved problems relating to the more general case of interacting fields that may or may not be adequately described by perturbation theory. For more on this topic, see Haag's theorem.
Physical meaning of particle indistinguishability
The second quantization procedure relies crucially on the particles being identical. We would not have been able to construct a quantum field theory from a distinguishable many-particle system, because there would have been no way of separating and indexing the degrees of freedom.
Many physicists prefer to take the converse interpretation, which is that quantum field theory explains what identical particles are. In ordinary quantum mechanics, there is not much theoretical motivation for using symmetric (bosonic) or antisymmetric (fermionic) states, and the need for such states is simply regarded as an empirical fact. From the point of view of quantum field theory, particles are identical if and only if they are excitations of the same underlying quantum field. Thus, the question "why are all electrons identical?" arises from mistakenly regarding individual electrons as fundamental objects, when in fact it is only the electron field that is fundamental.
Particle conservation and non-conservation
During second quantization, we started with a Hamiltonian and state space describing a fixed number of particles ( ), and ended with a Hamiltonian and state space for an arbitrary number of particles. Of course, in many common situations
), and ended with a Hamiltonian and state space for an arbitrary number of particles. Of course, in many common situations  is an important and perfectly well-defined quantity, e.g. if we are describing a gas of atoms sealed in a box. From the point of view of quantum field theory, such situations are described by quantum states that are eigenstates of the number operator
is an important and perfectly well-defined quantity, e.g. if we are describing a gas of atoms sealed in a box. From the point of view of quantum field theory, such situations are described by quantum states that are eigenstates of the number operator 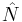 , which measures the total number of particles present. As with any quantum mechanical observable,
, which measures the total number of particles present. As with any quantum mechanical observable, 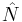 is conserved if it commutes with the Hamiltonian. In that case, the quantum state is trapped in the
is conserved if it commutes with the Hamiltonian. In that case, the quantum state is trapped in the  -particle subspace of the total Fock space, and the situation could equally well be described by ordinary
-particle subspace of the total Fock space, and the situation could equally well be described by ordinary  -particle quantum mechanics. (Strictly speaking, this is only true in the noninteracting case or in the low energy density limit of renormalized quantum field theories)
-particle quantum mechanics. (Strictly speaking, this is only true in the noninteracting case or in the low energy density limit of renormalized quantum field theories)
For example, we can see that the free-boson Hamiltonian described above conserves particle number. Whenever the Hamiltonian operates on a state, each particle destroyed by an annihilation operator 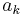 is immediately put back by the creation operator
is immediately put back by the creation operator 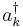 .
.
On the other hand, it is possible, and indeed common, to encounter quantum states that are not eigenstates of 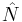 , which do not have well-defined particle numbers. Such states are difficult or impossible to handle using ordinary quantum mechanics, but they can be easily described in quantum field theory as quantum superpositions of states having different values of
, which do not have well-defined particle numbers. Such states are difficult or impossible to handle using ordinary quantum mechanics, but they can be easily described in quantum field theory as quantum superpositions of states having different values of  . For example, suppose we have a bosonic field whose particles can be created or destroyed by interactions with a fermionic field. The Hamiltonian of the combined system would be given by the Hamiltonians of the free boson and free fermion fields, plus a "potential energy" term such as
. For example, suppose we have a bosonic field whose particles can be created or destroyed by interactions with a fermionic field. The Hamiltonian of the combined system would be given by the Hamiltonians of the free boson and free fermion fields, plus a "potential energy" term such as
where 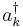 and
and 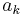 denotes the bosonic creation and annihilation operators,
denotes the bosonic creation and annihilation operators, 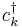 and
and 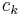 denotes the fermionic creation and annihilation operators, and
denotes the fermionic creation and annihilation operators, and 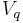 is a parameter that describes the strength of the interaction. This "interaction term" describes processes in which a fermion in state
is a parameter that describes the strength of the interaction. This "interaction term" describes processes in which a fermion in state 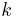 either absorbs or emits a boson, thereby being kicked into a different eigenstate
either absorbs or emits a boson, thereby being kicked into a different eigenstate 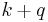 . (In fact, this type of Hamiltonian is used to describe interaction between conduction electrons and phonons in metals. The interaction between electrons and photons is treated in a similar way, but is a little more complicated because the role of spin must be taken into account.) One thing to notice here is that even if we start out with a fixed number of bosons, we will typically end up with a superposition of states with different numbers of bosons at later times. The number of fermions, however, is conserved in this case.
. (In fact, this type of Hamiltonian is used to describe interaction between conduction electrons and phonons in metals. The interaction between electrons and photons is treated in a similar way, but is a little more complicated because the role of spin must be taken into account.) One thing to notice here is that even if we start out with a fixed number of bosons, we will typically end up with a superposition of states with different numbers of bosons at later times. The number of fermions, however, is conserved in this case.
In condensed matter physics, states with ill-defined particle numbers are particularly important for describing the various superfluids. Many of the defining characteristics of a superfluid arise from the notion that its quantum state is a superposition of states with different particle numbers. In addition, the concept of a coherent state (used to model the laser and the BCS ground state) refers to a state with an ill-defined particle number but a well-defined phase.
Axiomatic approaches
The preceding description of quantum field theory follows the spirit in which most physicists approach the subject. However, it is not mathematically rigorous. Over the past several decades, there have been many attempts to put quantum field theory on a firm mathematical footing by formulating a set of axioms for it. These attempts fall into two broad classes.
The first class of axioms, first proposed during the 1950s, include the Wightman, Osterwalder-Schrader, and Haag-Kastler systems. They attempted to formalize the physicists' notion of an "operator-valued field" within the context of functional analysis, and enjoyed limited success. It was possible to prove that any quantum field theory satisfying these axioms satisfied certain general theorems, such as the spin-statistics theorem and the CPT theorem. Unfortunately, it proved extraordinarily difficult to show that any realistic field theory, including the Standard Model, satisfied these axioms. Most of the theories that could be treated with these analytic axioms were physically trivial, being restricted to low-dimensions and lacking interesting dynamics. The construction of theories satisfying one of these sets of axioms falls in the field of constructive quantum field theory. Important work was done in this area in the 1970s by Segal, Glimm, Jaffe and others.
During the 1980s, a second set of axioms based on geometric ideas was proposed. This line of investigation, which restricts its attention to a particular class of quantum field theories known as topological quantum field theories, is associated most closely with Michael Atiyah and Graeme Segal, and was notably expanded upon by Edward Witten, Richard Borcherds, and Maxim Kontsevich. However, most of the physically relevant quantum field theories, such as the Standard Model, are not topological quantum field theories; the quantum field theory of the fractional quantum Hall effect is a notable exception. The main impact of axiomatic topological quantum field theory has been on mathematics, with important applications in representation theory, algebraic topology, and differential geometry.
Finding the proper axioms for quantum field theory is still an open and difficult problem in mathematics. One of the Millennium Prize Problems—proving the existence of a mass gap in Yang-Mills theory—is linked to this issue.
Phenomena associated with quantum field theory
In the previous part of the article, we described the most general properties of quantum field theories. Some of the quantum field theories studied in various fields of theoretical physics possess additional special properties, such as renormalizability, gauge symmetry, and supersymmetry. These are described in the following sections.
Renormalization
Early in the history of quantum field theory, it was found that many seemingly innocuous calculations, such as the perturbative shift in the energy of an electron due to the presence of the electromagnetic field, give infinite results. The reason is that the perturbation theory for the shift in an energy involves a sum over all other energy levels, and there are infinitely many levels at short distances that each give a finite contribution.
Many of these problems are related to failures in classical electrodynamics that were identified but unsolved in the 19th century, and they basically stem from the fact that many of the supposedly "intrinsic" properties of an electron are tied to the electromagnetic field that it carries around with it. The energy carried by a single electron— its self energy— is not simply the bare value, but also includes the energy contained in its electromagnetic field, its attendant cloud of photons. The energy in a field of a spherical source diverges in both classical and quantum mechanics, but as discovered by Weisskopf, in quantum mechanics the divergence is much milder, going only as the logarithm of the radius of the sphere.
The solution to the problem, presciently suggested by Stueckelberg, independently by Bethe after the crucial experiment by Lamb, implemented at one loop by Schwinger, and systematically extended to all loops by Feynman and Dyson, with converging work by Tomonaga in isolated postwar Japan, is called renormalization. The technique of renormalization recognizes that the problem is essentially purely mathematical, that extremely short distances are at fault. In order to define a theory on a continuum, first place a cutoff on the fields, by postulating that quanta cannot have energies above some extremely high value. This has the effect of replacing continuous space by a structure where very short wavelengths do not exist, as on a lattice. Lattices break rotational symmetry, and one of the crucial contributions made by Feynman, Pauli and Villars, and modernized by 't Hooft and Veltman, is a symmetry preserving cutoff for perturbation theory. There is no known symmetrical cutoff outside of perturbation theory, so for rigorous or numerical work people often use an actual lattice.
On a lattice, every quantity is finite but depends on the spacing. When taking the limit of zero spacing, we make sure that the physically observable quantities like the observed electron mass stay fixed, which means that the constants in the Lagrangian defining the theory depend on the spacing. Hopefully, by allowing the constants to vary with the lattice spacing, all the results at long distances become insensitive to the lattice, defining a continuum limit.
The renormalization procedure only works for a certain class of quantum field theories, called renormalizable quantum field theories. A theory is perturbatively renormalizable when the constants in the Lagrangian only diverge at worst as logarithms of the lattice spacing for very short spacings. The continuum limit is then well defined in perturbation theory, and even if it is not fully well defined non-perturbatively, the problems only show up at distance scales that are exponentially small in the inverse coupling for weak couplings. The Standard Model of particle physics is perturbatively renormalizable, and so are its component theories (quantum electrodynamics/electroweak theory and quantum chromodynamics). Of the three components, quantum electrodynamics is believed to not have a continuum limit, while the asymptotically free SU(2) and SU(3) weak hypercharge and strong color interactions are nonperturbatively well defined.
The renormalization group describes how renormalizable theories emerge as the long distance low-energy effective field theory for any given high-energy theory. Because of this, renormalizable theories are insensitive to the precise nature of the underlying high-energy short-distance phenomena. This is a blessing because it allows physicists to formulate low energy theories without knowing the details of high energy phenomenon. It is also a curse, because once a renormalizable theory like the standard model is found to work, it gives very few clues to higher energy processes. The only way high energy processes can be seen in the standard model is when they allow otherwise forbidden events, or if they predict quantitative relations between the coupling constants.
Gauge freedom
A gauge theory is a theory that admits a symmetry with a local parameter. For example, in every quantum theory the global phase of the wave function is arbitrary and does not represent something physical. Consequently, the theory is invariant under a global change of phases (adding a constant to the phase of all wave functions, everywhere); this is a global symmetry. In quantum electrodynamics, the theory is also invariant under a local change of phase, that is - one may shift the phase of all wave functions so that the shift may be different at every point in space-time. This is a local symmetry. However, in order for a well-defined derivative operator to exist, one must introduce a new field, the gauge field, which also transforms in order for the local change of variables (the phase in our example) not to affect the derivative. In quantum electrodynamics this gauge field is the electromagnetic field. The change of local gauge of variables is termed gauge transformation.
In quantum field theory the excitations of fields represent particles. The particle associated with excitations of the gauge field is the gauge boson, which is the photon in the case of quantum electrodynamics.
The degrees of freedom in quantum field theory are local fluctuations of the fields. The existence of a gauge symmetry reduces the number of degrees of freedom, simply because some fluctuations of the fields can be transformed to zero by gauge transformations, so they are equivalent to having no fluctuations at all, and they therefore have no physical meaning. Such fluctuations are usually called "non-physical degrees of freedom" or gauge artifacts; usually some of them have a negative norm, making them inadequate for a consistent theory. Therefore, if a classical field theory has a gauge symmetry, then its quantized version (i.e. the corresponding quantum field theory) will have this symmetry as well. In other words, a gauge symmetry cannot have a quantum anomaly. If a gauge symmetry is anomalous (i.e. not kept in the quantum theory) then the theory is non-consistent: for example, in quantum electrodynamics, had there been a gauge anomaly, this would require the appearance of photons with longitudinal polarization and polarization in the time direction, the latter having a negative norm, rendering the theory inconsistent; another possibility would be for these photons to appear only in intermediate processes but not in the final products of any interaction, making the theory non unitary and again inconsistent (see optical theorem).
In general, the gauge transformations of a theory consist of several different transformations, which may not be commutative. These transformations are together described by a mathematical object known as a gauge group. Infinitesimal gauge transformations are the gauge group generators. Therefore the number of gauge bosons is the group dimension (i.e. number of generators forming a basis).
All the fundamental interactions in nature are described by gauge theories. These are:
- Quantum electrodynamics, whose gauge transformation is a local change of phase, so that the gauge group is U(1). The gauge boson is the photon.
- Quantum chromodynamics, whose gauge group is SU(3). The gauge bosons are eight gluons.
- The electroweak Theory, whose gauge group is
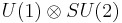 (a direct product of U(1) and SU(2)).
(a direct product of U(1) and SU(2)). - Gravity, whose classical theory is general relativity, admits the equivalence principle, which is a form of gauge symmetry. However, it is explicitly non-renormalizable.
Multivalued Gauge Transformations
The gauge transformations which leave the theory invariant involve by definition only single-valued gauge functions 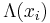 which satisfy the Schwarz integrability criterion
which satisfy the Schwarz integrability criterion
An interesting extension of gauge transformations arises if the gauge functions 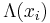 are allowed to be mutivalued functions which violate the integrability criterion. These are capable of changing the physical field strengths and are therefore no proper symmetry transformations. Nevertheless, the transformed field equations describe correctly the physical laws in the presence of the newly generated field strengths. See the textbook by H. Kleinert cited below for the applications to phenomena in physics.
are allowed to be mutivalued functions which violate the integrability criterion. These are capable of changing the physical field strengths and are therefore no proper symmetry transformations. Nevertheless, the transformed field equations describe correctly the physical laws in the presence of the newly generated field strengths. See the textbook by H. Kleinert cited below for the applications to phenomena in physics.
Supersymmetry
Supersymmetry assumes that every fundamental fermion has a superpartner that is a boson and vice versa. It was introduced in order to solve the so-called Hierarchy Problem, that is, to explain why particles not protected by any symmetry (like the Higgs boson) do not receive radiative corrections to its mass driving it to the larger scales (GUT, Planck...). It was soon realized that supersymmetry has other interesting properties: its gauged version is an extension of general relativity (Supergravity), and it is a key ingredient for the consistency of string theory.
The way supersymmetry protects the hierarchies is the following: since for every particle there is a superpartner with the same mass, any loop in a radiative correction is cancelled by the loop corresponding to its superpartner, rendering the theory UV finite.
Since no superpartners have yet been observed, if supersymmetry exists it must be broken (through a so-called soft term, which breaks supersymmetry without ruining its helpful features). The simplest models of this breaking require that the energy of the superpartners not be too high; in these cases, supersymmetry is expected to be observed by experiments at the Large Hadron Collider.
See also
|
|
Notes
- ↑ Weinberg, S. Quantum Field Theory, Vols. I to III, 2000, Cambridge University Press: Cambridge, UK.
- ↑ [1]
- ↑ Dirac, P.A.M. (1927). The Quantum Theory of the Emission and Absorption of Radiation, Proceedings of the Royal Society of London, Series A, Vol. 114, p. 243.
- ↑ Abraham Pais, Inward Bound: Of Matter and Forces in the Physical World ISBN 0-19-851997-4. Pais recounts how his astonishment at the rapidity with which Feynman could calculate using his method. Feynman's method is now part of the standard methods for physicists.
Further reading
General readers:
- Feynman, R.P. (2001) [1964]. The Character of Physical Law. MIT Press. ISBN 0262560038.
- Feynman, R.P. (2006) [1985]. QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 0691125759.
- Gribbin, J. (1998). Q is for Quantum: Particle Physics from A to Z. Weidenfeld & Nicolson. ISBN 0297817523.
- Schumm, Bruce A. (2004) Deep Down Things. Johns Hopkins Univ. Press. Chpt. 4.
Introductory texts:
- Bogoliubov, N.; Shirkov, D. (1982). Quantum Fields. Benjamin-Cummings. ISBN 0805309837.
- Frampton, P.H. (2000). Gauge Field Theories. Frontiers in Physics (2nd ed.). Wiley.
- Greiner, W; Müller, B. (2000). Gauge Theory of Weak Interactions. Springer. ISBN 3-540-67672-4.
- Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory. McGraw-Hill. ISBN 0-07-032071-3.
- Kane, G.L. (1987). Modern Elementary Particle Physics. Perseus Books. ISBN 0-201-11749-5.
- Kleinert, H.; Schulte-Frohlinde, Verena (2001). Critical Properties of φ4-Theories. World Scientific. ISBN 981-02-4658-7. http://users.physik.fu-berlin.de/~kleinert/re.html#B6.
- Kleinert, H. (2008). Multivalued Fields in Condensed Matter, Electrodynamics, and Gravitation. World Scientific. ISBN 978-981-279-170-2. http://users.physik.fu-berlin.de/~kleinert/public_html/kleiner_reb11/psfiles/mvf.pdf.
- Loudon, R (1983). The Quantum Theory of Light. Oxford University Press. ISBN 0-19-851155-8.
- Mandl, F.; Shaw, G. (1993). Quantum Field Theory. John Wiley & Sons. ISBN 0-0471-94186-7.
- Peskin, M.; Schroeder, D. (1995). An Introduction to Quantum Field Theory. Westview Press. ISBN 0-201-50397-2.
- Ryder, L.H. (1985). Quantum Field Theory. Cambridge University Press. ISBN 0-521-33859-X.
- Srednicki, Mark (2007) Quantum Field Theory. Cambridge Univ. Press.
- Yndurain, F.J. (1996). Relativistic Quantum Mechanics and Introduction to Field Theory (1st ed.). Springer. ISBN 978-3540604532.
- Zee, A. (2003). Quantum Field Theory in a Nutshell. Princeton University Press. ISBN ISBN 0-691-01019-6.
Advanced texts:
- Bogoliubov, N.; Logunov, A.A.; Oksak, A.I.; Todorov, I.T. (1990). General Principles of Quantum Field Theory. Kluwer Academic Publishers. ISBN 978-0792305408.
- Weinberg, S. (1995). The Quantum Theory of Fields. 1–3. Cambridge University Press.
Articles:
- Gerard 't Hooft (2007) "The Conceptual Basis of Quantum Field Theory" in Butterfield, J., and John Earman, eds., Philosophy of Physics, Part A. Elsevier: 661-730.
- Frank Wilczek (1999) "Quantum field theory," Reviews of Modern Physics 71: S83-S95. Also doi=10.1103/Rev. Mod. Phys. 71 .
External links
- Stanford Encyclopedia of Philosophy: "Quantum Field Theory," by Meinard Kuhlmann.
- Siegel, Warren, 2005. Fields. A free text, also available from arXiv:hep-th/9912205.
- Pedagogic Aids to Quantum Field Theory. Click on "Introduction" for a simplified introduction suitable for someone familiar with quantum mechanics.
- Free condensed matter books and notes.
- Quantum field theory texts, a list with links to amazon.com.
- Quantum Field Theory by P. J. Mulders
- Quantum Field Theory by David Tong
- Quantum Field Theory Video Lectures by David Tong
- Quantum Field Theory Lecture Notes by Michael Luke
- Quantum Field Theory Video Lectures by Sidney R. Coleman
- Quantum Field Theory Lecture Notes by D.J. Miller
- Quantum Field Theory Lecture Notes II by D.J. Miller
|
|||||
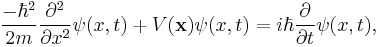
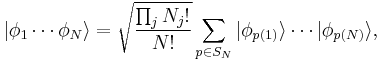
![\frac{1}{\sqrt{3}} \left[ |\phi_1\rang |\phi_2\rang
|\phi_2\rang + |\phi_2\rang |\phi_1\rang |\phi_2\rang + |\phi_2\rang
|\phi_2\rang |\phi_1\rang \right].](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/bcf4b3959ab6a5fc63d7af3d82631509.png)
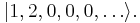
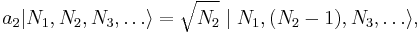
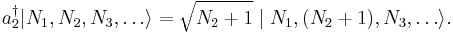
![\left[a_i , a_j \right] = 0 \quad,\quad
\left[a_i^\dagger , a_j^\dagger \right] = 0 \quad,\quad
\left[a_i , a_j^\dagger \right] = \delta_{ij},](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/2d745f427d9a6ce0351d39932145d907.png)
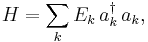
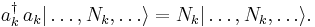
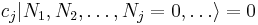
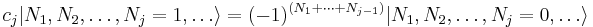
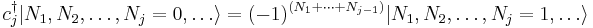
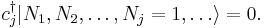
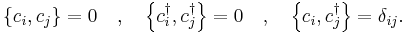
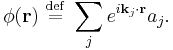
![\left[\phi(\mathbf{r}) , \phi(\mathbf{r'}) \right] = 0 \quad,\quad
\left[\phi^\dagger(\mathbf{r}) , \phi^\dagger(\mathbf{r'}) \right] = 0 \quad,\quad
\left[\phi(\mathbf{r}) , \phi^\dagger(\mathbf{r'}) \right] = \delta^3(\mathbf{r} - \mathbf{r'})](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/fc9f56a13d2847b019da3150d4165ba7.png)